💡Okay, so I have this problem about computers connected by cables, and a hacker cutting some cables to create 8 clusters. I need to find the maximum number of cables that could have been cut. Let me try to break this down step by step.First, there are 200 computers connected by 345 cables. Initially, all these computers form one big cluster, meaning every computer is connected to every other computer, either directly or through intermediate computers. Then, a hacker cuts some cables, and this causes the network to split into 8 separate clusters.I need to figure out the maximum number of cables that could have been cut. To do this, I think I need to understand how cutting cables affects the number of clusters. Each time a cable is cut, it might increase the number of clusters by one, but it depends on which cable is cut. If the cable was the only connection between two parts of the network, then cutting it would split the network into two clusters. But if there are multiple connections between two parts, cutting one cable might not increase the number of clusters.So, to maximize the number of cables cut, I want to minimize the number of cables that need to remain to keep the network connected as 8 clusters. In other words, I want to find the minimum number of cables required to keep the network as 8 clusters, and then subtract that from the original number of cables to find out how many were cut.I remember that in graph theory, a connected graph with n nodes has at least n-1 edges. This is called a tree. If you have more edges than that, the graph becomes redundant, meaning there are multiple paths between some nodes. So, for 8 clusters, each cluster can be thought of as a connected component. To have 8 clusters, we need to have 8 connected components.Each connected component (cluster) must have at least as many edges as the number of nodes minus one. So, if I denote the number of nodes in each cluster as n1, n2, ..., n8, then the minimum number of edges required to keep these clusters connected is (n1 - 1) + (n2 - 1) + ... + (n8 - 1) = (n1 + n2 + ... + n8) - 8. Since the total number of nodes is 200, this simplifies to 200 - 8 = 192 edges.So, the minimum number of edges needed to keep the network as 8 clusters is 192. Therefore, the maximum number of cables that could have been cut is the original number of cables minus this minimum, which is 345 - 192 = 153.Wait, let me double-check that. If we have 8 clusters, each cluster needs to be a connected component. The minimum number of edges for each cluster is (number of nodes in cluster - 1). So, adding that up for all clusters gives 200 - 8 = 192 edges. Therefore, the maximum number of edges that can be cut is 345 - 192 = 153. That seems right.But just to make sure, let me think about it another way. If I have 200 computers and I want to split them into 8 clusters, I need to remove enough cables so that there are no connections between these clusters. Each time I cut a cable that connects two different clusters, I can potentially increase the number of clusters by one. But to get from 1 cluster to 8 clusters, I need to make 7 cuts that each split a cluster into two. However, that's the minimum number of cuts needed to split into 8 clusters. But in reality, the hacker could have cut more cables, as long as the clusters remain connected within themselves.But wait, the problem is asking for the maximum number of cables that were cut, not the minimum. So, to maximize the number of cables cut, we need to minimize the number of cables remaining. The minimum number of cables remaining is 192, as calculated before. Therefore, the maximum number of cables cut is 345 - 192 = 153.Yes, that makes sense. So, the answer should be 153.

💡Okay, so I have this problem here: find the minimum value of the quadratic function ( 3x^2 - 18x + 2023 ). Hmm, I remember that quadratic functions have either a minimum or maximum value depending on the coefficient of ( x^2 ). Since the coefficient here is 3, which is positive, the parabola opens upwards, meaning it has a minimum point. Cool, so I need to find that minimum value.First, I think there are a couple of ways to approach this. One way is to complete the square, which I remember from algebra class. Another method is using calculus, finding the derivative and setting it to zero to find the critical point. But since this is a quadratic, maybe completing the square is simpler without needing calculus.Let me try completing the square. The function is ( 3x^2 - 18x + 2023 ). I notice that the coefficient of ( x^2 ) isn't 1; it's 3. So, I should factor out the 3 from the first two terms to make completing the square easier. Let's see:( y = 3x^2 - 18x + 2023 )Factor out 3 from the first two terms:( y = 3(x^2 - 6x) + 2023 )Okay, now inside the parentheses, I have ( x^2 - 6x ). To complete the square, I need to add and subtract the square of half the coefficient of x. The coefficient of x is -6, so half of that is -3, and squaring it gives 9. So, I'll add and subtract 9 inside the parentheses:( y = 3(x^2 - 6x + 9 - 9) + 2023 )Wait, that's a bit confusing. Let me rewrite it:( y = 3[(x^2 - 6x + 9) - 9] + 2023 )Simplify that:( y = 3(x - 3)^2 - 27 + 2023 )Because ( x^2 - 6x + 9 ) is a perfect square, which is ( (x - 3)^2 ). Then, distributing the 3 over the -9 gives me -27. Now, combine the constants:( y = 3(x - 3)^2 + (2023 - 27) )( y = 3(x - 3)^2 + 1996 )Alright, so now the function is in vertex form, which is ( y = a(x - h)^2 + k ), where (h, k) is the vertex. Since the coefficient a is positive, the vertex is the minimum point. Therefore, the minimum value of the function is k, which is 1996.Wait, let me double-check my steps to make sure I didn't make any mistakes. Factoring out the 3 was correct. Completing the square by adding and subtracting 9 inside the parentheses seems right. Then, simplifying to get ( 3(x - 3)^2 - 27 + 2023 ) and combining constants gives 1996. Yeah, that seems correct.Alternatively, I could use the formula for the vertex of a parabola. The x-coordinate of the vertex is at ( -b/(2a) ) for a quadratic ( ax^2 + bx + c ). Let me try that method to confirm.Given the quadratic ( 3x^2 - 18x + 2023 ), so a = 3, b = -18. Plugging into the formula:( x = -(-18)/(2*3) = 18/6 = 3 )So, the x-coordinate of the vertex is 3. To find the minimum value, substitute x = 3 back into the original equation:( y = 3(3)^2 - 18(3) + 2023 )Calculate each term:( 3(9) = 27 )( -18(3) = -54 )So, ( y = 27 - 54 + 2023 )Combine the constants:27 - 54 = -27Then, -27 + 2023 = 1996Same result! So, that confirms it. The minimum value is indeed 1996.I think I've got it right. Both methods lead me to the same answer, so I'm confident that 1996 is the minimum value of the function.

💡Alright, so I've got this problem here: there are 2017 points on a plane, and no three of them are collinear. We're supposed to look at all the triangles formed by these points and figure out that the number of "good" triangles—those with the largest area—can't exceed 2017. Hmm, okay, let's break this down.First off, I need to understand what makes a triangle "good." It's one that has the maximum area among all possible triangles formed by these points. So, if I imagine all these points scattered on a plane, the good triangles are the ones that are as large as possible. That probably means they're using points that are spread out as much as possible.Now, the problem is asking me to prove that there can't be more than 2017 of these good triangles. That seems a bit abstract. Maybe I can approach this by thinking about how these triangles are formed. Each triangle is made by three points, so the number of possible triangles is huge—like, combinatorially huge, since it's 2017 choose 3. But we're only concerned with the ones that have the maximum area.I wonder if there's a way to relate the number of these maximum area triangles to the number of points. Maybe something with convex hulls? Because the convex hull of a set of points is the smallest convex polygon that contains all the points, and the points on the convex hull are the ones that are "extreme" in some sense. Maybe the maximum area triangles are formed by points on the convex hull.Wait, but the problem doesn't mention anything about convex hulls, so maybe I'm overcomplicating it. Let's think simpler. If I have a set of points, and I want to form triangles with the largest area, those triangles must have their vertices as far apart as possible. So, perhaps each good triangle uses two points that are the farthest apart, and then a third point that's as far as possible from that line.But then, how many such triangles can I have? If I fix two points as the base, how many different third points can give me the maximum area? Well, the area of a triangle is (base * height)/2, so for a fixed base, the height is determined by the distance from the third point to the line formed by the base. So, to maximize the area, the third point must be as far as possible from that line.If I have multiple points that are all equally far from the base line, then each of those points would form a triangle with the same maximum area. But the problem states that no three points are collinear, so those third points can't all lie on a single line parallel to the base. Hmm, that might limit the number of such points.Wait, but if I have multiple points that are all at the same maximum distance from the base line, they can't be collinear, so they must lie on different lines parallel to the base. But how many such points can I have? If I have too many, then maybe I can form too many good triangles, which would contradict the problem statement.But I'm not sure if that's the right path. Maybe I should think about the number of pairs of points. There are 2017 points, so the number of pairs is 2017 choose 2, which is a lot. Each pair can be the base for potentially multiple good triangles, depending on how many points are at the maximum height from that base.But the problem says that the number of good triangles can't exceed 2017. So, maybe each pair can only be the base for a limited number of good triangles. If I can show that each pair can only be the base for one good triangle, then the total number of good triangles would be at most 2017 choose 2, which is way more than 2017. So that approach doesn't help.Wait, maybe it's not about the pairs, but about something else. Maybe each good triangle shares a common edge or something. Or perhaps each good triangle must include a specific point. Hmm, not sure.Let me think about extremal cases. Suppose all the points are on a convex polygon. Then, the maximum area triangles would be those that use three consecutive vertices or something like that. But no, actually, the maximum area triangle in a convex polygon is usually formed by three vertices that are as far apart as possible.But in a convex polygon with n vertices, how many maximum area triangles can you have? I think it's n, because for each vertex, there's a unique triangle that includes it and two other vertices that maximize the area. But I'm not entirely sure.Wait, in a regular polygon, the maximum area triangles are those that are formed by vertices that are equally spaced. For example, in a regular hexagon, the maximum area triangles are those that skip two vertices each time. But in that case, how many such triangles are there? It's equal to the number of vertices, right? Because each vertex is part of exactly one such triangle.So, maybe in general, for a convex polygon with n vertices, the number of maximum area triangles is n. If that's the case, then in our problem, since we have 2017 points, and assuming they form a convex polygon, the number of good triangles would be 2017.But the problem doesn't specify that the points are in convex position. They could be in any configuration, as long as no three are collinear. So, maybe the maximum number of good triangles is related to the number of points on the convex hull.But again, the problem doesn't mention convex hulls, so maybe I'm overcomplicating it. Let's try a different approach.Suppose that there are more than 2017 good triangles. Each good triangle has three vertices. So, if there are more than 2017 triangles, then by the pigeonhole principle, some points must be used multiple times. But how does that help?Wait, maybe if I consider that each good triangle must have a certain property, like being part of the convex hull or something. If I can show that each good triangle must include a unique point, then the number of good triangles can't exceed the number of points.But I'm not sure. Maybe I need to think about the areas. Since all good triangles have the same maximum area, maybe their configurations are constrained in some way.Let me think about the area formula again. The area of a triangle is (base * height)/2. So, for a fixed base, the height is determined by the distance from the third point to the line of the base. To maximize the area, we need to maximize the height.So, for a given pair of points, the third point that maximizes the area is the one farthest from the line connecting the first two. Now, if there are multiple points that are equally far from that line, then each of those points would form a triangle with the same maximum area.But the problem states that no three points are collinear, so those multiple points can't lie on a single line parallel to the base. So, they must lie on different lines, each parallel to the base, but at the same maximum distance.But how many such points can there be? If I have too many, then I might be able to form too many good triangles, which would contradict the problem statement.Wait, but if I have multiple points at the same maximum distance from the base, each of those points would form a good triangle with the base. So, if I have k such points, I would have k good triangles with that base.But then, if I have too many such bases, the total number of good triangles could exceed 2017.Hmm, maybe I need to consider that each good triangle must have a unique base or something. Or perhaps that each good triangle must include a unique point.Wait, another idea: if I have a set of points, the maximum area triangle must have its vertices on the convex hull. Because if a point is inside the convex hull, then you can always find a triangle with a larger area by replacing that point with one on the hull.So, maybe all good triangles must have their vertices on the convex hull. If that's the case, then the number of good triangles is limited by the number of points on the convex hull.But again, the problem doesn't specify anything about the convex hull, so maybe that's not the right path.Wait, but even if all good triangles are on the convex hull, the number of such triangles could still be more than 2017, depending on the shape of the hull.Hmm, I'm stuck. Maybe I need to think about this differently. Let's suppose that there are more than 2017 good triangles. Then, since each triangle has three points, by the pigeonhole principle, some points must be used in multiple good triangles.But how does that lead to a contradiction? Maybe if a point is used in too many good triangles, it implies that there are multiple points at the same maximum distance from some line, which would mean they're collinear, contradicting the given condition.Wait, that might be something. Let me try to formalize that.Suppose there are more than 2017 good triangles. Then, since there are 2017 points, by the pigeonhole principle, at least one point must be part of at least two good triangles. But actually, it's more precise: the number of incidences between points and good triangles is 3 times the number of good triangles. So, if there are more than 2017 good triangles, then the total number of incidences is more than 3*2017. Since there are only 2017 points, by the pigeonhole principle, some point must be part of at least 3 good triangles.So, suppose point A is part of three good triangles: ABC, ABD, and ABE. Now, since all these triangles are good, they all have the same maximum area. So, the area of ABC, ABD, and ABE are all equal.Now, let's think about the area of these triangles. The area of ABC is (1/2)*base*height, where the base could be AB, and the height is the distance from C to the line AB. Similarly for ABD and ABE.Since all these areas are equal, the heights from C, D, and E to the line AB must be equal. So, points C, D, and E must all lie on a line parallel to AB at the same distance from AB.But wait, the problem states that no three points are collinear. So, if C, D, and E are all on the same line parallel to AB, then they would be collinear, which contradicts the given condition.Therefore, our assumption that there are more than 2017 good triangles must be false. Hence, there cannot be more than 2017 good triangles.Yeah, that seems to make sense. By assuming there are more than 2017 good triangles, we end up forcing three points to be collinear, which contradicts the problem's condition. So, the maximum number of good triangles must be at most 2017.

💡Okay, so I need to find the focus of the parabola given by the equation ( y = 9x^2 + 5 ). Hmm, I remember that parabolas have something called a focus, which is a specific point that helps define the shape of the parabola. But I'm a bit fuzzy on the exact method to find it. Let me try to recall.First, I think the standard form of a parabola is important here. I remember that a parabola can be expressed in the form ( y = ax^2 + bx + c ), which is a quadratic equation. In this case, the given equation is ( y = 9x^2 + 5 ). I notice that there's no ( x ) term, so ( b = 0 ). That might simplify things.I also recall that the standard form of a parabola that opens upwards or downwards is ( y = a(x - h)^2 + k ), where ( (h, k) ) is the vertex of the parabola. Comparing this to the given equation ( y = 9x^2 + 5 ), it seems like ( h = 0 ) and ( k = 5 ). So the vertex of this parabola is at ( (0, 5) ). That makes sense because when ( x = 0 ), ( y = 5 ).Now, I need to find the focus. I think the focus is located at a certain distance from the vertex along the axis of symmetry of the parabola. Since this parabola opens upwards (because the coefficient of ( x^2 ) is positive), the focus will be above the vertex.I remember there's a formula related to the coefficient ( a ) that helps find the distance from the vertex to the focus. I think it's ( frac{1}{4a} ). Let me check if that sounds right. If ( a ) is the coefficient of ( x^2 ), then yes, the distance from the vertex to the focus is ( frac{1}{4a} ).In this equation, ( a = 9 ). So plugging that into the formula, the distance should be ( frac{1}{4 times 9} = frac{1}{36} ). That seems very small, but I think it's correct because the parabola is quite narrow due to the large coefficient ( a = 9 ).Since the vertex is at ( (0, 5) ) and the focus is ( frac{1}{36} ) units above the vertex, I can find the coordinates of the focus by adding ( frac{1}{36} ) to the ( y )-coordinate of the vertex. So, the ( y )-coordinate of the focus is ( 5 + frac{1}{36} ).To add these together, I need to express 5 as a fraction with a denominator of 36. 5 is equal to ( frac{180}{36} ), so adding ( frac{1}{36} ) gives ( frac{181}{36} ). Therefore, the focus is at ( (0, frac{181}{36}) ).Wait, let me double-check my steps to make sure I didn't make a mistake. The standard form is correct, and I identified the vertex correctly. The formula for the distance from the vertex to the focus is ( frac{1}{4a} ), which I applied correctly with ( a = 9 ). Adding that distance to the vertex's ( y )-coordinate also seems right.Just to be thorough, I'll recall that for a parabola in the form ( y = ax^2 + bx + c ), the focus can be found using the formula ( (h, k + frac{1}{4a}) ), where ( h ) and ( k ) are the coordinates of the vertex. Since ( h = 0 ) and ( k = 5 ), the focus is indeed ( (0, 5 + frac{1}{36}) ), which simplifies to ( (0, frac{181}{36}) ).I think that's it. I can't see any errors in my reasoning, so I'm confident that the focus of the parabola ( y = 9x^2 + 5 ) is at ( (0, frac{181}{36}) ).

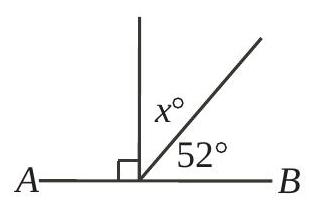
💡Okay, so I have this geometry problem here where AB is a line segment, and I need to find the value of x. The options are 128, 38, 48, 142, and 308. Hmm, let me try to visualize the diagram they provided. Since I can't see the actual image, I'll have to rely on the description and the information given.First, AB is a line segment, which means it's a straight line. In geometry, when we have a straight line, the sum of the angles on one side of the line should be 180 degrees because they form a linear pair. So, if there are angles formed by points on AB, their measures should add up to 180 degrees.Looking at the problem, it mentions angles ACD, DCE, and ECB. I think these are angles formed by points C, D, and E on the line AB. So, point C is somewhere on AB, and from C, there are lines going to points D and E, creating angles at point C. Specifically, angle ACD is 90 degrees, angle DCE is x, and angle ECB is 52 degrees.Let me write this down:- Angle ACD = 90 degrees- Angle DCE = x degrees- Angle ECB = 52 degreesSince these three angles are on the straight line AB, their sum should be 180 degrees. So, I can set up the equation:90 degrees + x + 52 degrees = 180 degreesNow, let's solve for x. First, combine the known angles:90 + 52 = 142So, the equation becomes:142 + x = 180To find x, subtract 142 from both sides:x = 180 - 142x = 38So, x should be 38 degrees. Let me check the answer choices:(A) 128(B) 38(C) 48(D) 142(E) 30838 is option B. That seems to make sense because 90 + 38 + 52 equals 180, which fits the linear pair condition.Wait, just to make sure I didn't make any mistakes. Let me go through the steps again.1. AB is a straight line, so the sum of angles on one side is 180 degrees.2. The angles given are ACD = 90°, DCE = x°, and ECB = 52°.3. Adding them up: 90 + x + 52 = 180.4. Combine 90 and 52: 142 + x = 180.5. Subtract 142 from both sides: x = 38.Yes, that all checks out. I don't think I made any calculation errors. So, x is definitely 38 degrees.I wonder if there's another way to approach this problem. Maybe using triangle properties or something else? Let me think. If points D and E are on AB, then maybe triangles ACD and ECB are right triangles since angle ACD is 90 degrees. But I don't have any information about the sides or other angles in those triangles, so I don't think that approach would help here.Alternatively, if I consider the angles around point C, since AB is a straight line, the angles on one side should add up to 180 degrees. That's exactly what I did earlier, so I think that's the correct method.Another thing to consider is whether the diagram might have any other information or if there are any other angles that I might have missed. But based on the problem statement, it only mentions these three angles: ACD, DCE, and ECB. So, I think focusing on those three is the right approach.Just to be thorough, let me visualize the line AB with point C somewhere in the middle. From C, there are two lines: one going to D, forming a 90-degree angle with AC, and another going to E, forming a 52-degree angle with CB. The angle between CD and CE is x degrees. Since all these angles are on the same side of AB, they should add up to 180 degrees.So, 90 degrees (ACD) + x degrees (DCE) + 52 degrees (ECB) = 180 degrees. Solving for x gives 38 degrees, which is one of the answer choices. That seems consistent.I don't see any other angles or information that could affect this calculation. It doesn't mention anything about vertical angles or other lines intersecting, so I think the initial approach is correct.In summary, by recognizing that the angles on a straight line add up to 180 degrees, I was able to set up an equation and solve for x. The answer is 38 degrees, which is option B.

💡Alright, so I have this problem about a line on the Cartesian plane, specifically ( y = x + frac{1}{sqrt{2}} ). There are two parts: part (a) asks me to prove that every circle with center on this line and radius ( frac{1}{8} ) has no integral points inside. Part (b) is about finding the greatest ( k > 0 ) such that the distance from every integral point to the line ( d ) is at least ( k ).Starting with part (a). I need to show that such circles don't contain any integral points inside them. Integral points are points where both coordinates are integers, like (1,2), (0,0), etc. So, if I can show that the distance from any integral point to the line ( d ) is always greater than ( frac{1}{8} ), then it would mean that no integral point lies inside any of these circles.Wait, actually, the radius is ( frac{1}{8} ), so if the distance from an integral point to the center of the circle is less than ( frac{1}{8} ), then the point would lie inside the circle. But since the center is on the line ( d ), the distance from the integral point to the line ( d ) is related to the distance from the point to the center.Hmm, maybe I should first figure out the distance from an integral point to the line ( d ). If I can find a lower bound for this distance, then I can compare it to ( frac{1}{8} ). If the minimum distance is greater than ( frac{1}{8} ), then no integral point can be inside any such circle.So, let me recall the formula for the distance from a point ( (x_0, y_0) ) to the line ( ax + by + c = 0 ). It's ( frac{|ax_0 + by_0 + c|}{sqrt{a^2 + b^2}} ). For the line ( y = x + frac{1}{sqrt{2}} ), I can rewrite it as ( x - y + frac{1}{sqrt{2}} = 0 ). So, ( a = 1 ), ( b = -1 ), and ( c = frac{1}{sqrt{2}} ).Therefore, the distance from an integral point ( (m, n) ) to the line ( d ) is ( frac{|m - n + frac{1}{sqrt{2}}|}{sqrt{1 + 1}} = frac{|m - n + frac{1}{sqrt{2}}|}{sqrt{2}} ).Now, ( m ) and ( n ) are integers, so ( m - n ) is also an integer. Let's denote ( k = m - n ), which is an integer. Then the distance becomes ( frac{|k + frac{1}{sqrt{2}}|}{sqrt{2}} ).I need to find the minimum value of this expression over all integers ( k ). Since ( frac{1}{sqrt{2}} ) is approximately 0.707, the closest integers to ( -frac{1}{sqrt{2}} ) are -1 and 0. So, let's compute the distance for ( k = -1 ) and ( k = 0 ).For ( k = -1 ): ( | -1 + 0.707 | = | -0.293 | = 0.293 ). Divided by ( sqrt{2} ), that's approximately ( 0.293 / 1.414 approx 0.207 ).For ( k = 0 ): ( | 0 + 0.707 | = 0.707 ). Divided by ( sqrt{2} ), that's ( 0.707 / 1.414 approx 0.5 ).So, the minimum distance is approximately 0.207, which is greater than ( frac{1}{8} = 0.125 ). Therefore, the distance from any integral point to the line ( d ) is at least approximately 0.207, which is greater than ( frac{1}{8} ). Hence, no integral point can lie inside any circle of radius ( frac{1}{8} ) centered on ( d ). That proves part (a).Moving on to part (b). I need to find the greatest ( k > 0 ) such that the distance from every integral point to ( d ) is at least ( k ). From the previous calculation, I saw that the minimum distance is approximately 0.207, which is ( frac{sqrt{2} - 1}{2} ). Let me verify that.Wait, ( sqrt{2} approx 1.414 ), so ( sqrt{2} - 1 approx 0.414 ). Divided by 2, that's approximately 0.207. Yes, that matches my earlier calculation. So, the minimum distance is indeed ( frac{sqrt{2} - 1}{2} ).But let me think more carefully. Is this the exact value? Let's compute ( frac{sqrt{2} - 1}{2} ). It is approximately 0.207, as I said. Is this the minimal distance?Yes, because when ( k = -1 ), the distance is ( frac{| -1 + frac{1}{sqrt{2}} |}{sqrt{2}} = frac{1 - frac{1}{sqrt{2}}}{sqrt{2}} = frac{sqrt{2} - 1}{2} ).So, that's the minimal distance. Therefore, the greatest ( k ) such that every integral point is at least ( k ) away from ( d ) is ( frac{sqrt{2} - 1}{2} ).I think that's it. So, part (a) is proved by showing the minimal distance is greater than ( frac{1}{8} ), and part (b) identifies that minimal distance as ( frac{sqrt{2} - 1}{2} ).