💡First, I need to evaluate ( f(-1) ). Since (-1) is less than (0), I use the second part of the piecewise function:[f(-1) = 2^{-1} = frac{1}{2}]Next, I need to evaluate ( fleft(frac{1}{2}right) ). Since (frac{1}{2}) is greater than or equal to (0), I use the first part of the piecewise function:[fleft(frac{1}{2}right) = left(frac{1}{2}right)^2 = frac{1}{4}]Therefore, ( f[f(-1)] = frac{1}{4} ).

💡Alright, so I need to find the smallest sum of five consecutive prime numbers that is divisible by three. Hmm, okay. Let's start by recalling what prime numbers are. Primes are numbers greater than 1 that have no divisors other than 1 and themselves. So, the sequence of prime numbers starts like 2, 3, 5, 7, 11, 13, 17, and so on.Now, the problem is asking for five consecutive primes, meaning I need to pick five primes in a row from this list and add them up. Then, I need to check if that sum is divisible by three. If it is, that's my answer. If not, I'll move to the next set of five consecutive primes and repeat the process until I find the smallest such sum.Let me start with the smallest primes to see if their sum is divisible by three. The first five primes are 2, 3, 5, 7, and 11. Let's add them up:2 + 3 + 5 + 7 + 11 = 28.Okay, now I need to check if 28 is divisible by three. To do that, I can divide 28 by 3 and see if there's a remainder. 3 times 9 is 27, which is less than 28, and 3 times 10 is 30, which is more than 28. So, 28 divided by 3 is 9 with a remainder of 1. That means 28 is not divisible by three.Alright, so the first set of five consecutive primes doesn't work. Let's move to the next set. The next five primes after 2, 3, 5, 7, 11 are 3, 5, 7, 11, and 13. Let's add those up:3 + 5 + 7 + 11 + 13 = 39.Now, checking if 39 is divisible by three. Well, 3 times 13 is 39, so yes, it is divisible by three. That seems promising. But wait, is this the smallest sum? I need to make sure there isn't a smaller set of five consecutive primes that adds up to a number divisible by three.Wait a minute, the first set started with 2, and the second set started with 3. Since 2 is the smallest prime, the first set is indeed the smallest possible set of five consecutive primes. But since its sum wasn't divisible by three, the next possible set is the one starting with 3, which gave us 39. So, 39 seems to be the smallest sum that meets the criteria.But just to be thorough, let me check the next few sets to make sure I'm not missing something. The next set after 3, 5, 7, 11, 13 would be 5, 7, 11, 13, 17. Let's add those:5 + 7 + 11 + 13 + 17 = 53.53 divided by 3 is approximately 17.666..., which means it's not divisible by three. So, that doesn't work either.Next set: 7, 11, 13, 17, 19.7 + 11 + 13 + 17 + 19 = 67.67 divided by 3 is about 22.333..., so again, not divisible by three.Continuing on, the next set is 11, 13, 17, 19, 23.11 + 13 + 17 + 19 + 23 = 83.83 divided by 3 is roughly 27.666..., which isn't a whole number. So, not divisible by three.Next set: 13, 17, 19, 23, 29.13 + 17 + 19 + 23 + 29 = 101.101 divided by 3 is about 33.666..., still not divisible by three.Hmm, seems like 39 is the only sum so far that's divisible by three. Let me just go back and make sure I didn't skip any sets or make a calculation error.First set: 2, 3, 5, 7, 11 = 28 (not divisible by three).Second set: 3, 5, 7, 11, 13 = 39 (divisible by three).Third set: 5, 7, 11, 13, 17 = 53 (not divisible).Fourth set: 7, 11, 13, 17, 19 = 67 (not divisible).Fifth set: 11, 13, 17, 19, 23 = 83 (not divisible).Sixth set: 13, 17, 19, 23, 29 = 101 (not divisible).Seventh set: 17, 19, 23, 29, 31.17 + 19 + 23 + 29 + 31 = 119.119 divided by 3 is about 39.666..., not divisible.Eighth set: 19, 23, 29, 31, 37.19 + 23 + 29 + 31 + 37 = 139.139 divided by 3 is approximately 46.333..., not divisible.Ninth set: 23, 29, 31, 37, 41.23 + 29 + 31 + 37 + 41 = 161.161 divided by 3 is about 53.666..., not divisible.Tenth set: 29, 31, 37, 41, 43.29 + 31 + 37 + 41 + 43 = 181.181 divided by 3 is roughly 60.333..., not divisible.Eleventh set: 31, 37, 41, 43, 47.31 + 37 + 41 + 43 + 47 = 199.199 divided by 3 is approximately 66.333..., not divisible.Twelfth set: 37, 41, 43, 47, 53.37 + 41 + 43 + 47 + 53 = 221.221 divided by 3 is about 73.666..., not divisible.Thirteenth set: 41, 43, 47, 53, 59.41 + 43 + 47 + 53 + 59 = 243.Wait a minute, 243 divided by 3 is exactly 81. So, 243 is divisible by three.But hold on, I already found that the sum starting at 3 is 39, which is much smaller than 243. So, 39 is definitely smaller. Therefore, 39 is the smallest sum of five consecutive primes divisible by three.But just to be absolutely sure, let me check if there's any set between the second set and the thirteenth set that I might have missed or miscalculated.Looking back:After the second set (sum 39), the next sets all had sums not divisible by three until the thirteenth set, which gave 243. Since 39 is smaller than 243, and all the sums in between weren't divisible by three, 39 must be the smallest such sum.Therefore, the smallest sum of five consecutive prime numbers that is divisible by three is 39.

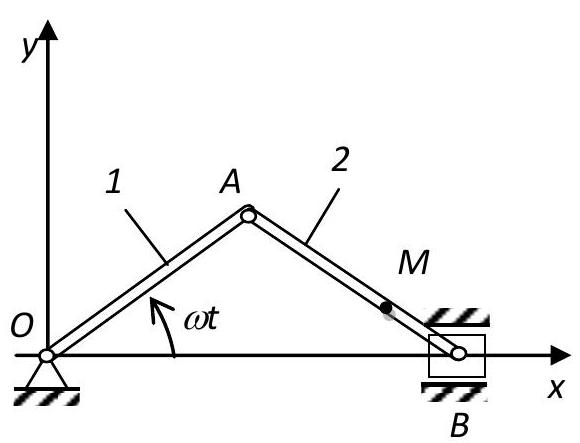
💡Okay, so I have this problem about a crank-slider mechanism, which was used in Roman sawmills. The crank rotates with a constant angular velocity of 10 rad/s. I need to find the equations of motion, the trajectory equation, and the speed of point M on the connecting rod. The lengths given are OA = AB = 90 cm, and MB is one-third of AB, which would be 30 cm.First, I should probably visualize the mechanism. There's a crank OA, which is rotating, connected to a connecting rod AB, which in turn is connected to a slider at point B. Point M is somewhere along the connecting rod AB, specifically one-third of the way from B.Since the crank is rotating with a constant angular velocity, I can describe the motion of point A using trigonometric functions. Let me denote the angle of rotation of the crank OA as θ(t) = ωt, where ω is 10 rad/s. So, θ(t) = 10t.The coordinates of point A can be given in terms of θ(t). Since OA is 90 cm, the x-coordinate of A is 90 cos(θ(t)) and the y-coordinate is 90 sin(θ(t)). So, A is (90 cos(10t), 90 sin(10t)).Now, point B is constrained to move along the x-axis because it's a slider. Let's denote the x-coordinate of B as x_B(t). Since AB is 90 cm, the distance between A and B must always be 90 cm. So, using the distance formula, the distance between A and B is sqrt[(x_B - 90 cos(10t))^2 + (0 - 90 sin(10t))^2] = 90.Squaring both sides to eliminate the square root gives:(x_B - 90 cos(10t))^2 + (90 sin(10t))^2 = 90^2.Expanding this, we get:x_B^2 - 180 x_B cos(10t) + (90 cos(10t))^2 + (90 sin(10t))^2 = 90^2.Simplify the terms:x_B^2 - 180 x_B cos(10t) + 90^2 (cos^2(10t) + sin^2(10t)) = 90^2.Since cos^2 + sin^2 = 1, this simplifies to:x_B^2 - 180 x_B cos(10t) + 90^2 = 90^2.Subtracting 90^2 from both sides:x_B^2 - 180 x_B cos(10t) = 0.Factor out x_B:x_B (x_B - 180 cos(10t)) = 0.So, x_B = 0 or x_B = 180 cos(10t). Since x_B = 0 would mean the slider isn't moving, which isn't the case, we take x_B = 180 cos(10t).Now, point M is one-third of the way from B to A along the connecting rod AB. So, to find the coordinates of M, I can use the section formula. Since M divides AB in the ratio 2:1 (because MB is one-third of AB), the coordinates of M can be found by:x_M = (2 * x_B + 1 * x_A) / (2 + 1) = (2x_B + x_A)/3.Similarly,y_M = (2 * y_B + 1 * y_A) / 3.But y_B is 0 because B is on the x-axis. So,y_M = (0 + y_A)/3 = y_A / 3.Substituting the coordinates of A and B:x_M = (2 * 180 cos(10t) + 90 cos(10t)) / 3 = (360 cos(10t) + 90 cos(10t)) / 3 = 450 cos(10t) / 3 = 150 cos(10t).y_M = (90 sin(10t)) / 3 = 30 sin(10t).Wait, that doesn't seem right. If M is one-third from B, shouldn't the y-coordinate be one-third of A's y-coordinate? Let me double-check.Yes, since M is closer to B, its y-coordinate should be one-third of A's y-coordinate. So, y_M = (1/3) * y_A = (1/3) * 90 sin(10t) = 30 sin(10t). That makes sense.But for the x-coordinate, since M is closer to B, it should be closer to x_B. So, x_M should be x_B minus one-third of the distance from B to A in the x-direction. The distance from B to A in the x-direction is x_A - x_B. So, x_M = x_B + (1/3)(x_A - x_B).Let me recalculate:x_M = x_B + (1/3)(x_A - x_B) = (2/3)x_B + (1/3)x_A.Plugging in x_A = 90 cos(10t) and x_B = 180 cos(10t):x_M = (2/3)(180 cos(10t)) + (1/3)(90 cos(10t)) = 120 cos(10t) + 30 cos(10t) = 150 cos(10t).Okay, that matches what I had before. So, x_M = 150 cos(10t) and y_M = 30 sin(10t).Wait, but earlier I thought y_M was 90 sin(10t). That was a mistake. It should be 30 sin(10t) because M is one-third from B, so it's one-third the height of A.Now, for the trajectory equation, we can eliminate the parameter t from the equations of x_M and y_M.We have:x = 150 cos(10t),y = 30 sin(10t).Let me write cos(10t) = x / 150,and sin(10t) = y / 30.Since cos^2(10t) + sin^2(10t) = 1,(x / 150)^2 + (y / 30)^2 = 1.So, the trajectory is an ellipse given by:(x^2)/(150^2) + (y^2)/(30^2) = 1.Now, for the velocity of point M, we need to find the derivatives of x_M and y_M with respect to time.v_x = dx/dt = -150 * 10 sin(10t) = -1500 sin(10t),v_y = dy/dt = 30 * 10 cos(10t) = 300 cos(10t).So, the velocity vector is (-1500 sin(10t), 300 cos(10t)).But wait, earlier I thought y_M was 90 sin(10t), but corrected it to 30 sin(10t). So, the velocity in y-direction is 300 cos(10t).But let me double-check the differentiation:x = 150 cos(10t),dx/dt = -150 * 10 sin(10t) = -1500 sin(10t).y = 30 sin(10t),dy/dt = 30 * 10 cos(10t) = 300 cos(10t).Yes, that's correct.So, the speed of point M is the magnitude of the velocity vector:Speed = sqrt[(-1500 sin(10t))^2 + (300 cos(10t))^2] = sqrt[(2250000 sin^2(10t)) + (90000 cos^2(10t))].We can factor out 90000:sqrt[90000(25 sin^2(10t) + cos^2(10t))] = 300 sqrt(25 sin^2(10t) + cos^2(10t)).But that's the speed as a function of time. If we want the maximum speed or something else, we might need to analyze further, but the problem just asks for the speed, so this expression is sufficient.Wait, but the problem says "the speed of point M". It might be asking for the instantaneous speed, which is the magnitude of the velocity vector, which I've expressed above. Alternatively, if it's asking for the velocity components, then it's (-1500 sin(10t), 300 cos(10t)).I think the problem wants both the equations of motion (which are x(t) and y(t)), the trajectory equation (the ellipse), and the speed, which is the magnitude of the velocity.So, summarizing:Equations of motion:x(t) = 150 cos(10t),y(t) = 30 sin(10t).Trajectory equation:(x^2)/(150^2) + (y^2)/(30^2) = 1.Speed:v(t) = sqrt[(-1500 sin(10t))^2 + (300 cos(10t))^2] = 300 sqrt(25 sin^2(10t) + cos^2(10t)).Alternatively, we can write it as:v(t) = 300 sqrt(25 sin^2(10t) + cos^2(10t)).But perhaps we can simplify it further. Let's see:25 sin^2(10t) + cos^2(10t) = 24 sin^2(10t) + (sin^2(10t) + cos^2(10t)) = 24 sin^2(10t) + 1.So,v(t) = 300 sqrt(24 sin^2(10t) + 1).That might be a more compact form.Alternatively, we can factor out sin^2:v(t) = 300 sqrt(1 + 24 sin^2(10t)).Either way is acceptable.So, to recap:- Equations of motion: x = 150 cos(10t), y = 30 sin(10t).- Trajectory: (x^2)/22500 + (y^2)/900 = 1.- Speed: 300 sqrt(1 + 24 sin^2(10t)) cm/s.Wait, the units. Since OA is in cm, the coordinates are in cm, and angular velocity is in rad/s, so the speed will be in cm/s.Yes, that makes sense.I think that covers everything the problem is asking for.

💡Okay, so I have this problem here: Given that a is greater than b, which of the following relationships is definitely correct? The options are A, B, C, and D. Let me try to figure this out step by step.First, I know that a > b. That means a is to the right of b on the number line if we're talking about positive numbers, or maybe a is less negative than b if we're dealing with negative numbers. But I don't know the exact values of a and b, just that a is bigger than b.Let me look at each option one by one.**Option A: a² > b²**Hmm, this one is about squaring both a and b. I remember that squaring a number makes it positive, but does it always keep the inequality the same? Let me think. If both a and b are positive, then yes, squaring them would keep the inequality the same because multiplying two positive numbers maintains the order. For example, if a = 3 and b = 2, then 3² = 9 and 2² = 4, so 9 > 4, which holds true.But what if a and b are negative? Let's say a = -2 and b = -3. Here, a > b because -2 is greater than -3. But squaring them, (-2)² = 4 and (-3)² = 9, so 4 < 9. That means a² is actually less than b² in this case, which contradicts the original inequality. So, squaring doesn't always preserve the inequality if negative numbers are involved. Therefore, Option A isn't necessarily correct.**Option B: 2a < 2b**This one is about multiplying both sides of the inequality by 2. I recall that when you multiply or divide both sides of an inequality by a positive number, the direction of the inequality remains the same. So, if a > b, then multiplying both by 2 should give 2a > 2b, not 2a < 2b. For example, if a = 4 and b = 3, then 2a = 8 and 2b = 6, so 8 > 6, which means 2a > 2b. This contradicts Option B, which says 2a < 2b. So, Option B is definitely incorrect.**Option C: a + 2 < b + 2**This option is about adding 2 to both sides of the inequality. I remember that adding or subtracting the same number from both sides of an inequality doesn't change the direction of the inequality. So, if a > b, then adding 2 to both sides should give a + 2 > b + 2, not a + 2 < b + 2.Let me test this with numbers. If a = 5 and b = 4, then a + 2 = 7 and b + 2 = 6, so 7 > 6. Again, this contradicts Option C, which suggests a + 2 < b + 2. Therefore, Option C is also incorrect.**Option D: -a < -b**This one involves multiplying both sides of the inequality by -1. I remember that when you multiply or divide both sides of an inequality by a negative number, the direction of the inequality flips. So, if a > b, then multiplying both by -1 would give -a < -b.Let me verify this with some numbers. If a = 3 and b = 2, then -a = -3 and -b = -2. So, -3 < -2, which holds true. What if a and b are negative? Let's say a = -1 and b = -2. Here, a > b because -1 is greater than -2. Multiplying by -1, we get -a = 1 and -b = 2, so 1 < 2, which is still true. It seems like no matter what values a and b take, as long as a > b, multiplying both by -1 will always reverse the inequality, making -a < -b. Therefore, Option D is definitely correct.So, after analyzing all the options, only Option D holds true under the given condition that a > b.

💡Okay, so I have this problem about a parabola, and I need to figure out its equation. Let me try to understand what's given and what I need to find.The equation of the parabola is given as ( y^2 = 2px ) where ( p > 0 ). I remember that for a parabola in this form, it opens to the right because the coefficient of ( x ) is positive. The vertex of this parabola is at the origin (0,0), and the focus is at ( ( frac{p}{2}, 0 ) ). Wait, is that right? Let me think. Actually, for a standard parabola ( y^2 = 4ax ), the focus is at ( (a, 0) ). So comparing that to ( y^2 = 2px ), it seems like ( 4a = 2p ), which means ( a = frac{p}{2} ). So yes, the focus is at ( ( frac{p}{2}, 0 ) ).Now, the problem says there's a point ( M ) on the parabola with an x-coordinate of 3. So the coordinates of point ( M ) are ( (3, y) ). Since it's on the parabola, it must satisfy the equation ( y^2 = 2p times 3 ), which simplifies to ( y^2 = 6p ). So the y-coordinate(s) of point ( M ) are ( sqrt{6p} ) and ( -sqrt{6p} ). But I don't think the sign matters here because distance is always positive.Next, it says that the distance from ( M ) to the focus ( F ) is ( 2p ). The focus ( F ) is at ( ( frac{p}{2}, 0 ) ). So I need to find the distance between ( M(3, y) ) and ( F( frac{p}{2}, 0 ) ) and set that equal to ( 2p ).Let me write the distance formula. The distance between two points ( (x_1, y_1) ) and ( (x_2, y_2) ) is ( sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} ). Applying that here, the distance ( |MF| ) is:[sqrt{left( frac{p}{2} - 3 right)^2 + (0 - y)^2} = 2p]Simplify this equation. First, square both sides to eliminate the square root:[left( frac{p}{2} - 3 right)^2 + y^2 = (2p)^2]I know that ( y^2 = 6p ) from earlier, so I can substitute that into the equation:[left( frac{p}{2} - 3 right)^2 + 6p = 4p^2]Now, let's expand ( left( frac{p}{2} - 3 right)^2 ):[left( frac{p}{2} - 3 right)^2 = left( frac{p}{2} right)^2 - 2 times frac{p}{2} times 3 + 3^2 = frac{p^2}{4} - 3p + 9]So substitute back into the equation:[frac{p^2}{4} - 3p + 9 + 6p = 4p^2]Combine like terms:[frac{p^2}{4} + 3p + 9 = 4p^2]Let me get all terms to one side to solve for ( p ). Subtract ( frac{p^2}{4} + 3p + 9 ) from both sides:[0 = 4p^2 - frac{p^2}{4} - 3p - 9]Simplify ( 4p^2 - frac{p^2}{4} ). Let's convert 4p^2 to quarters: ( 4p^2 = frac{16p^2}{4} ). So:[0 = frac{16p^2}{4} - frac{p^2}{4} - 3p - 9 = frac{15p^2}{4} - 3p - 9]Multiply every term by 4 to eliminate the denominator:[0 = 15p^2 - 12p - 36]So now we have a quadratic equation:[15p^2 - 12p - 36 = 0]Let me try to simplify this equation. All coefficients are divisible by 3:[5p^2 - 4p - 12 = 0]Now, let's solve for ( p ) using the quadratic formula. The quadratic is ( 5p^2 - 4p - 12 = 0 ), so ( a = 5 ), ( b = -4 ), ( c = -12 ).The quadratic formula is:[p = frac{-b pm sqrt{b^2 - 4ac}}{2a}]Plugging in the values:[p = frac{-(-4) pm sqrt{(-4)^2 - 4 times 5 times (-12)}}{2 times 5} = frac{4 pm sqrt{16 + 240}}{10} = frac{4 pm sqrt{256}}{10}]Simplify ( sqrt{256} ):[sqrt{256} = 16]So,[p = frac{4 pm 16}{10}]This gives two solutions:1. ( p = frac{4 + 16}{10} = frac{20}{10} = 2 )2. ( p = frac{4 - 16}{10} = frac{-12}{10} = -1.2 )But the problem states that ( p > 0 ), so we discard the negative solution. Therefore, ( p = 2 ).Now, substitute ( p = 2 ) back into the equation of the parabola:[y^2 = 2px = 2 times 2 times x = 4x]So the equation of the parabola is ( y^2 = 4x ).Let me double-check my steps to make sure I didn't make a mistake.1. I found the focus correctly at ( (frac{p}{2}, 0) ).2. I used the distance formula between ( M(3, y) ) and ( F(frac{p}{2}, 0) ).3. Substituted ( y^2 = 6p ) into the distance equation.4. Expanded and simplified the equation correctly.5. Solved the quadratic equation and found ( p = 2 ).6. Plugged ( p = 2 ) back into the original equation.Everything seems to check out. So the correct equation is ( y^2 = 4x ), which is option B.**Final Answer**boxed{B}

💡Alright, so I have this equation: lg x + x = 3. Hmm, I need to find the interval where the solution lies. The options are from (0,1) up to (3,4). Let me think about how to approach this.First, I remember that lg x is the logarithm base 10 of x. So, lg x is only defined for x > 0. That means the domain of this equation is x > 0. Okay, so all the intervals given are within the domain, which is good.Now, I need to find x such that lg x + x = 3. Maybe I can define a function f(x) = lg x + x - 3. Then, finding the solution to the equation is equivalent to finding the root of f(x) = 0.Since f(x) is a combination of a logarithmic function and a linear function, I wonder if it's monotonic. If it is, then there will be only one solution. Let me check the derivative to see if it's always increasing or always decreasing.The derivative of f(x) with respect to x is f'(x) = derivative of lg x + derivative of x - derivative of 3. The derivative of lg x is 1/(x ln 10), and the derivative of x is 1. The derivative of a constant like 3 is 0. So, f'(x) = 1/(x ln 10) + 1.Since x > 0, both terms 1/(x ln 10) and 1 are positive. Therefore, f'(x) is always positive. That means f(x) is strictly increasing on its entire domain. So, there can only be one solution to f(x) = 0.Now, since f(x) is strictly increasing, I can use the Intermediate Value Theorem to find the interval where the solution lies. I need to evaluate f(x) at the endpoints of the given intervals and see where it changes sign.Let's start with option A: (0,1). Let me pick x = 1. f(1) = lg 1 + 1 - 3. Since lg 1 is 0, f(1) = 0 + 1 - 3 = -2. So, f(1) is negative. What about as x approaches 0 from the right? As x approaches 0, lg x approaches negative infinity, and x approaches 0. So, f(x) approaches negative infinity. Therefore, f(x) is negative throughout (0,1). So, there's no solution in (0,1). So, option A is out.Option B: (1,2). Let's evaluate f(1) and f(2). We already know f(1) = -2. What about f(2)? f(2) = lg 2 + 2 - 3. lg 2 is approximately 0.3010, so f(2) ≈ 0.3010 + 2 - 3 = -0.699. So, f(2) is still negative. Since f(x) is increasing, and both f(1) and f(2) are negative, there's no solution in (1,2). So, option B is also out.Option C: (2,3). Let's check f(2) and f(3). We already have f(2) ≈ -0.699. Now, f(3) = lg 3 + 3 - 3. lg 3 is approximately 0.4771, so f(3) ≈ 0.4771 + 3 - 3 = 0.4771. So, f(3) is positive. Since f(2) is negative and f(3) is positive, and f(x) is continuous and strictly increasing, by the Intermediate Value Theorem, there must be a solution in (2,3). So, option C is a candidate.Option D: (3,4). Let's check f(3) and f(4). We have f(3) ≈ 0.4771, which is positive. What about f(4)? f(4) = lg 4 + 4 - 3. lg 4 is approximately 0.6020, so f(4) ≈ 0.6020 + 4 - 3 = 1.6020. So, f(4) is still positive. Since f(x) is increasing and both f(3) and f(4) are positive, there's no solution in (3,4). So, option D is out.Therefore, the solution must lie in interval C: (2,3).I think that's it. I checked each interval by evaluating the function at the endpoints, used the fact that the function is strictly increasing, and applied the Intermediate Value Theorem to find where the function crosses zero. It makes sense because the function is always going up, so it can only cross the x-axis once, and that crossing is between 2 and 3.**Final Answer**boxed{C}